ShopKoreaOnline: The Best Source for K-Pop, K-Beauty, K-Food & K-Fashion
Affiliate Disclosure: When you click on links to various merchants on this site and make a purchase, this can result in this site earning a commission. Affiliate programs and affiliations include, but are not limited to, the eBay Partner Network.
K-POP UNIVERSE
Collect your favorite idols' albums and limited edition merchandise.

K-BEAUTY SECRETS
Discover glowing skin with trending Korean skincare and makeup.

K-FOOD PARADISE
Experience authentic Korean flavors with trending snacks and ramen.

K-FASHION TRENDS
Dress like a star with the latest Seoul street styles and accessories.
DISCOVER YOUR WORLD
Curated K-Pop, Beauty, Food & Fashion

OSHIAREE PST-Cell 6pc Full Skincare Set Anti-Aging Brightening Korean K-Beauty

16 x Samyang Buldak Hot Chicken Flavor Ramen (105g) from Korea

Acme De La Vie SEVENTEEN Hoshi Hoodie ADLV Korean Street Fashion K pop Rare

Korean Skincare Set The White Signature 6-Piece for Skin Whitening Wrinkle Care

24 x Samyang Buldak Hot Chicken Flavor Ramen (70g) from Korea

Seoul City Skyline Korean Culture T-Shirt Long Sleeve Soft Stretch Ivory Large
![New Jeans Photo Poster [10P Pack] (A4 Size) K-POP 2025.07](https://i.ebayimg.com/images/g/4dIAAOSw~oJnfnEd/s-l640.jpg)
New Jeans Photo Poster [10P Pack] (A4 Size) K-POP 2025.07

Ginseng Skincare Set Hyobidam Korean Skin Care Set k-beauty

16 x Samyang Buldak Carbonara Ramen (105g) from Korea

Seoul City Skyline Korean Culture T-Shirt Long Sleeve Stretchy Black X-Large

NewJeans - 2024 SEASON'S GREETINGS (SEALED) NEW JEANS K-POP / EMS SHIPPING

"Jennybell Snail Mucin Skincare Set – Korean Anti-Aging & Hydrating Face Cream"

24 x Samyang Buldak Carbonara Ramen (80g) from Korea

ByTheR Taegeuk Dragon Phoenix Neoprene Strap Hooded Zip-Up K-street style

New Jeans 12P Poster Pack (A3 Size) Bromide & Photo Sticker K-POP 2025.06

30PCS Korean Essence Facial Mask Sheets Nose Strip Set Moisture Face Mask Pack

Buldak Carbo Hot Chicken Flavor Ramen, 130g, Pack of 4

Korean street fashion brand MAHAGRID logo WHITE T-shirt Men's / unisex cotton
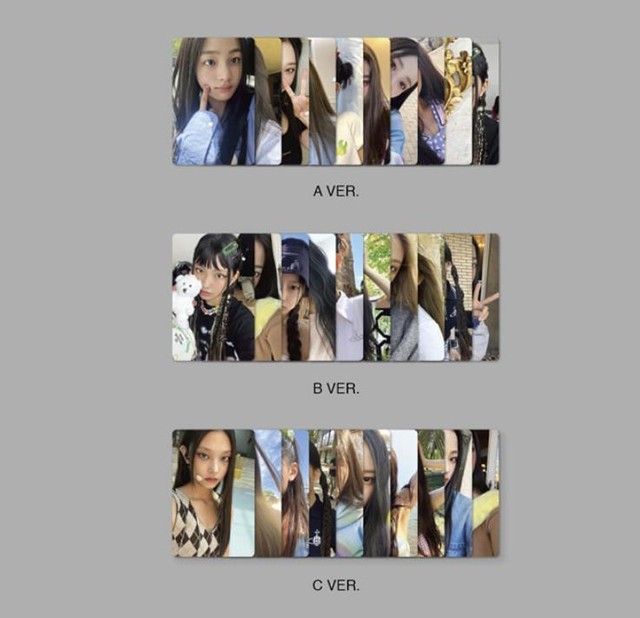
NewJeans 1st EP NEW JEANS K-POP Weverse Albums VER. + PHOTOCARD SET NEW

New Korean cosmetic samples Sets RANDOM SAMPLE Special Event Set Moisturizer

Samyang Buldak Sauce Original Extremely Spicy Carbo Chipotle Mayo Sriracha 200g

Covernat x Yosigo, Collabo, Korean-Streetwear, K-Fashion, Korea Brand, Authentic

NEW JEANS Official Authentic Photocard CRAZY ALADIN POB RARE - 6 TYPE

Sulwhasoo Firming Skincare Set - Toner, Emulsion, Ginseng Cream | Korean Beauty

40 x Samyang Buldak Hot Chicken Flavor Ramen (140g) from Korea

Seoul City Skyline Korean Culture T-Shirt Long Sleeve Eco Friendly Beige X-Large
![New Jeans[NJZ] Photo Calendar 2026 & 2027 K-POP 2025.06-1](https://i.ebayimg.com/images/g/ZEEAAeSwhb5oXrMc/s-l640.jpg)
New Jeans[NJZ] Photo Calendar 2026 & 2027 K-POP 2025.06-1

Korean Cosmetic AHC Vital Golden Collagen Skin care eye cream Special set

3 x Samyang Buldak Pu Pa Pong Curry Ramen (105g) from Korea

Seoul City Skyline Korean Culture T-Shirt Long Sleeve Stretchy Gray Large









